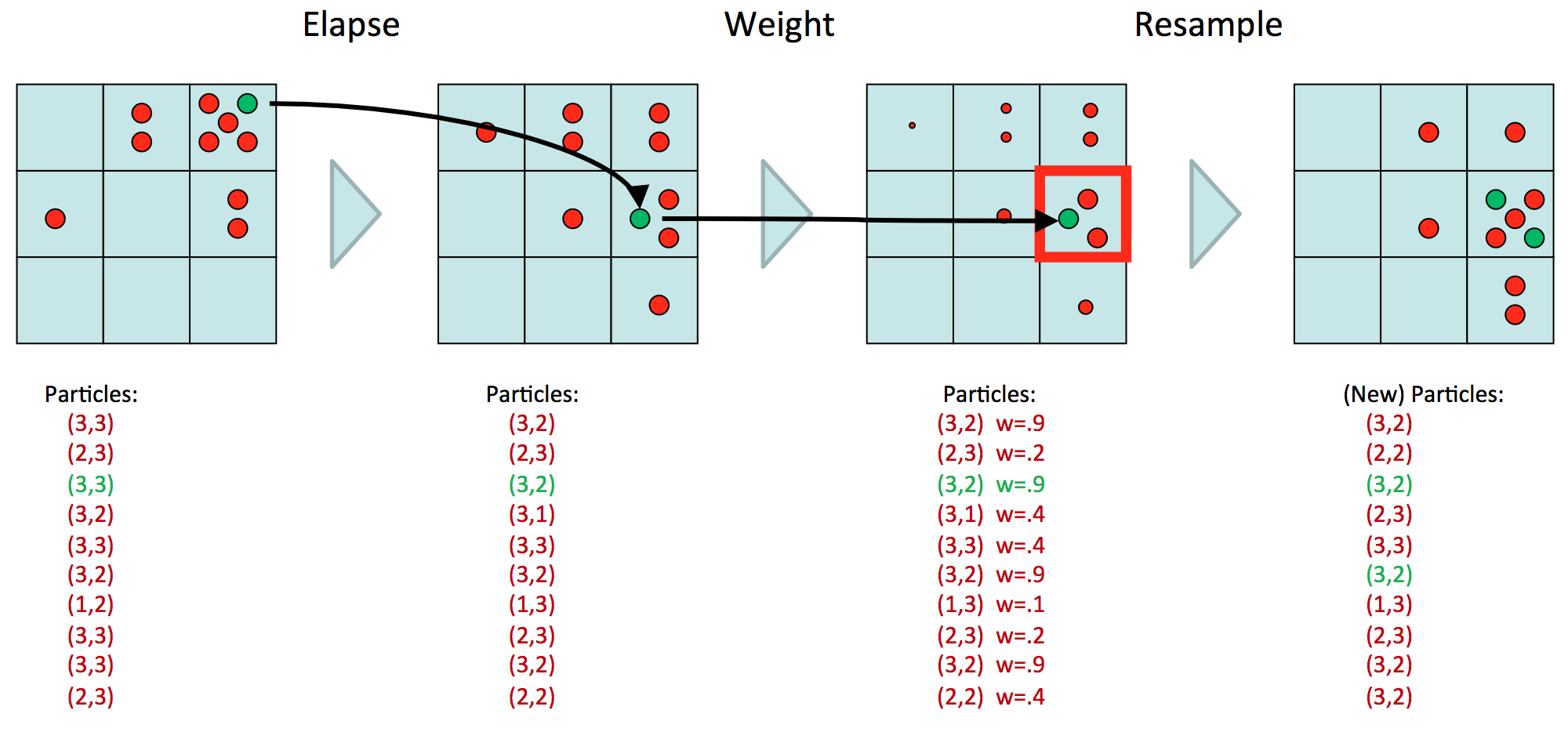
Description:
- Sometimes ∣X∣ is too big to use exact inference, might be even too big to store B(X)
- Approximate the probablity using particles instead of samples, n particles then each represents probability 1/n
- time per step is linear in the number of particles
- only particles and its position (states) are recorded, not states itself
- Used in Robot Localization
- Passage of time:
- Each particle is moved by sampling its next position from the transition model x′=sample(P(X′∣x))
- This captures the passage of time
- Observe:
- When observer, dont sample observation, fix it
- Similar to Likelihood Weighting, downweight the samples based on the evidence
- w(x)=P(e∣x)
- B(X)∝P(e∣X)B′(X)
- As before, the probabilities don’t sum to one, since all have been down-weighted (in fact they now sum to (N times) an approximation of P(e))
- Resample:
- Rather than tracking weighted samples, we resample
- N times, we choose from our weighted sample distribution (i.e. draw with replacement)
- This is equivalent to renormalizing the distribution
- Now the update is complete for this time step, continue with the next one
- Starting at frame k and after resample, we have state k+1