Backtracking Search

Description:

• The basic uninformed algorithm for solving CSPs
• We can use Filtering, Arc Consistency, Ordering with new heuristics and Structure exploiration to improve search

To form the search tree:

• Idea 1: One variable at a time
  • Variable assignment can be commutative so no ordering, ex: A = Red, B = Blue can be switched
  • Only need to consider assignments to a single variable at each step
• Idea 2: Check constraints as you go
  • Only consider the assignments that doesnt conflict with all the previous assignments
  • ie, “Incremental goal test”
• Therefore, each states has child states as possible assignments
  • 
• DFS with these 2 ideas are called Backtracking Search
• 

Filtering:

• Metareasoning
• Help detects inevitable failure early
• Forward Checking:
  • 
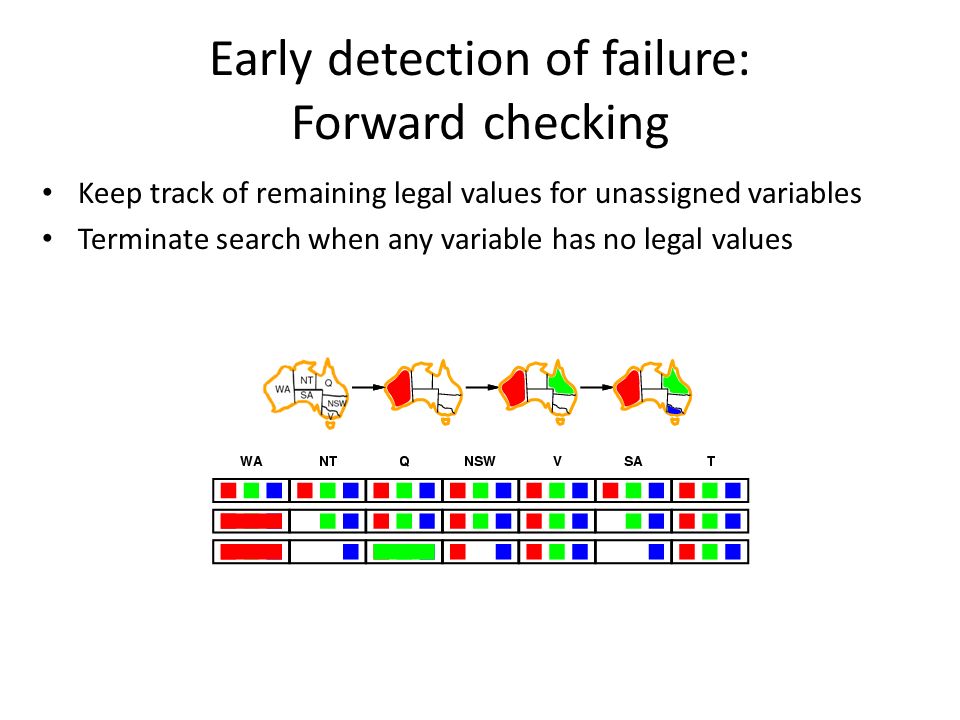
    • if we assign WA to red, then NT and SA cant be red
    • If we assign G to green then NT and NSW and SA cant be green
    • But SA and NT cant both be blue → terminate G to green (constraint propagation)
  • Propagates information from assigned to unassigned variables, but doesn’t provide early detection for all failures
  • Constrant Propagation: reason from constraint to constrant

Arc Consistency:

• $O(n^2{d}^3)$ can be reduced to $O(n^2{d}^2)$
• An arc X → Y is consistent iff for every value x there is some allowed value of y
• If it is violating, delete from the tail (the “from” node)
• If X loses a value, neighbors of X need to be rechecked!
• Therefore, detect failture faster than Filtering
• The Entire CSP is arc consistency if every arcs are consistent
• Can be run as a preprocessor or after each assignment
• Limitation:
  • Can also have multiple solution
  • Can have no solution but not knowing it
    • ex: A=R/B, B=R/B, C=R/B while ABC are connected
    • because they are only checked between 2 nodes at a time

K-consistency:

• 1-consistency: a node meets its own unary requirements
• 2-consistency: any 2 nodes are consistence, Arc Consistency
• 3-consistency: path consistency
• k-consistency: any k-nodes are consistence
  • more k → more expensive to compute
  • k-consistency also mean that k-1, k-2,k-3,… are also consistence

Ordering with new heuristics:

• Minimum Remaining Values (MRV) as a heuristic:
  • Which variable should be assigned next? (MRV)
  • Choose the variable with the fewest legal values left in its domain
    • ”most constrained variable”
  • if it gonna fail, reach failure faster
• Least Constraining Value as a heuristic:
  • What order should the values be tried? (LCV)
  • Determine which value has the least constraint
  • pick the value with the least so there is more options for other variables
  • Takes more computation
  • Increase likeliness of having solution
  • 1 value is less constrained than another by rerunning Filtering

Structure exploiration:

• We can exploit the structure to speed up the search

1. Independent subproblems:
   • if there are 2 disconnected subgraph, solve them independently can exponentially save time
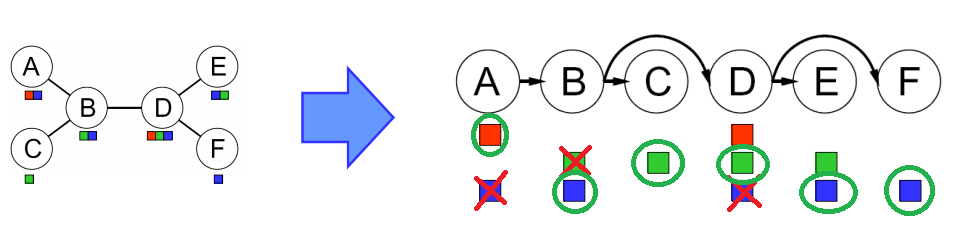
2. As a tree-structured:
   • theorem If the constrant graph has no loops, the CSP can be solved in $O(n{d}^2)$
     • Compared to general CSP, it is $O(d^n)$
   • Convert CSP to Tree Search
     • Ordering by choose a root variable, order variables so that parents precede children
       • 
     • Then remove backward, remove inconsistency
       • ex: F makes blue of D unavailable,B’s green unavailable, then A’s blue unavailable
     • Then assign forward, assign $X_i$ consistently with Parent of $X_i$
       • ex: A has to be red, B. has to B blue, C has to be green, D can be red or green, E is blue, F is blue
     • $O(n{d}^2)$
     • Why does it always work?
       • After backward pass. all root-to-leaf arcs are consistent
       • If root-to-leaf arcs are consistent, forward assignment do not need to backtrack
3. Near tree-structured:
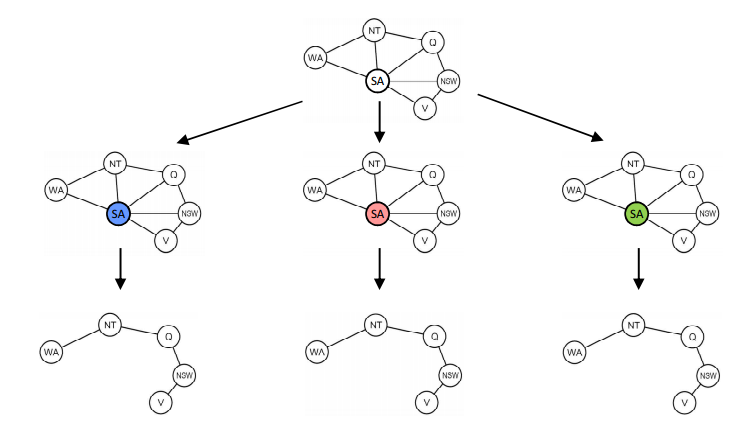
   • Conditioning: instantiate a variable, prune its neighbor domains
     • 
   • Cutset conditioning: have a set of variables such that the remaining constrant graph is a tree
     • Cutset size $c$ gives runtime O(create cutset * solve tree-structured CSP)= $O(d^c(n-c)d^2)$ which is very fast for small c
   • Steps:
     • create a set of possible nodes of cutset
     • if it is blue, al its neighbor cant be blue
     • Solve the rest of the nodes as tree

4. Tree decomposition: